三角形を成り立たせる3辺 (三角形の成立条件) 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a < bc; 三角形の公式が使える条件 c^2=a^2b^2 上記で、三角形の各辺の長さがわかる条件を教えてください。 ちょっと見た感じですと、どこか一つの内角が90度であればいいような気がするのですがどうでしょうか?正弦定理から,三角形の辺の長さを求める計算について ABCにおいてa = 3 ,A = 60°,B = 45°のときbを求めよ。 という問題がありますが, これを定理にあてはめていって, b = 3 / sin60°× sin45° まではつくれるんですが,そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが,意味がわかりま

高校 数学 三角比29 三角形の面積公式 8分 Youtube
不等辺三角形 辺の長さ 比
不等辺三角形 辺の長さ 比-正三角形の1辺の長さをaとするすると PB・a+PC・a=AP・a 次のように証明しても良い. BPCをBの周りに60°回転した三角形を BP'Aとする(上図). このとき, この命題は逆もなりたつ.すなわちでは、どう求めるか。 今分かっている情報は、 「1辺3角(c=6,A=60°,B=75°,C=45°)」 だよね。 1辺2角を使って他の辺の長さを求めるときには、 正弦定理 を突破口としよう。 aとbどちらから求めにいくのがいいかな? どちらも同じではないんだ。 aに対応する ∠Aは60° 、bに対応する ∠Bは75° だ。 sin60°なら計算できるけれど、sin75°の値は勉強していないよ。 という




黄金三角形による18 シリーズの三角比 おいしい数学
alp******** さん 18/4/3 850 公式として覚えているものはありませんが, 敢えて作るとすれば,以下のような感じかな? ABC につき,BC,CA,AB の長さをa,b,c とし s = (abc)/2 とおく。 aを底辺とみたときの高さを H (a) で表すと H (a) = (2/a)√ {s (sa) (sb) (sc)} alp******** alp******** さん 18/4/3 858 適当な内角がわかっていれば, もっと簡単ですけどね。直角三角形の2 辺の長さがわかれば,残りの辺の長さは,三平方の定理を利用して求めるこ とができる。直角をはさむ2 辺の長さをa,bとし,斜辺の長さをcとすると ・a,bが与えられたとき cab=+22 ・b,cが与えられたとき acb=-22 三平方の定理の逆 三角形の3 辺の長さa,b,cの間に不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C
三角不等式は様々な「長さ」に拡張されています。→いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc三角形の3辺の長さから面積を求めましょう お題の三角形については \a = 7,\quad b = 5,\quad c = 8\ が,分かっているということです どの角の大きさも分っていません んっ! 待ってください・・・この三角形は,どこかで見たことがあるような気がします3辺の長さだけがわかっている三角形の面積を求めるには、 (1)一旦、余弦定理で、ある角の cos を求める (2)次に sin 2 θ+cos 2 θ=1 の関係を使って sin を求める (3)2辺とその間の角の sin が判明したので、これを公式に当てはめる アプリもご利用
三角形の2辺の和と差 物理学のフィロ 直角三角形の高さは? 残り2辺の長さを求めることができます。 もちろん \(11\sqrt{2}\)や\(12\sqrt{3}\)という比は覚えておく必要があるからね。 しっかりと覚えておこう! では、特別な直角三角形において 比を使いながら辺の長さを求める練習をしていきましょう。 まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。



中学数学の面積比についての質問です 画像の問題で 1番と2番は Yahoo 知恵袋




黄金長方形 Wikipedia
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう! 「サイト内お気に入り」に登録する 数多の直角三角形のうち、二つの特別な直角三角形の三つの辺「底辺」「高さ」「斜辺」の長さの比の関係は簡単な数字で表される。 二つの特別な余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますが三角関数は,最初は直角三角形の一つの鋭角によって定まる辺の長さの比,いわゆる三角比として定義せられ,それが一般の角に拡張された。 それらに関して後述の加法定理などの性質や,別の項目で述べられる三角形の 正弦定理 , 余弦定理 が導かれ




三角形の七不思議 より 気になる文章




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学
不等辺三角形 著者名 著:内田 康夫 発売日 12年04月06日 価格 定価:1,122円(本体1,0円) isbn 9754 判型 新書 ページ数 296ページ シリーズ 講談社ノベルス 初出 10年4月に小社より単行本として刊行されたものを、ノベルス化したもの。BH=xとおいて (このときCH=6xとなります) AHの長さ (の2乗)を2とおりの方法で表わせば解けます。 (√13) 2 x 2 = AH 2 = 5 2 (6x) 2 (√13)2x2 = 52 (6x)2 13x 2 =25 (3612xx 2 ) 24=12x x=2 (√13) 2 2 2 =AH 2 AH=32 高さ (h) =SQRT (3)/2*B1 3 3辺の長さ (L) =3*B1 4 面積 (S) =SQRT (3)/4*B1^2




15 号 内燃機関の熱発生率波形作成装置および燃焼状態診断装置 Astamuse
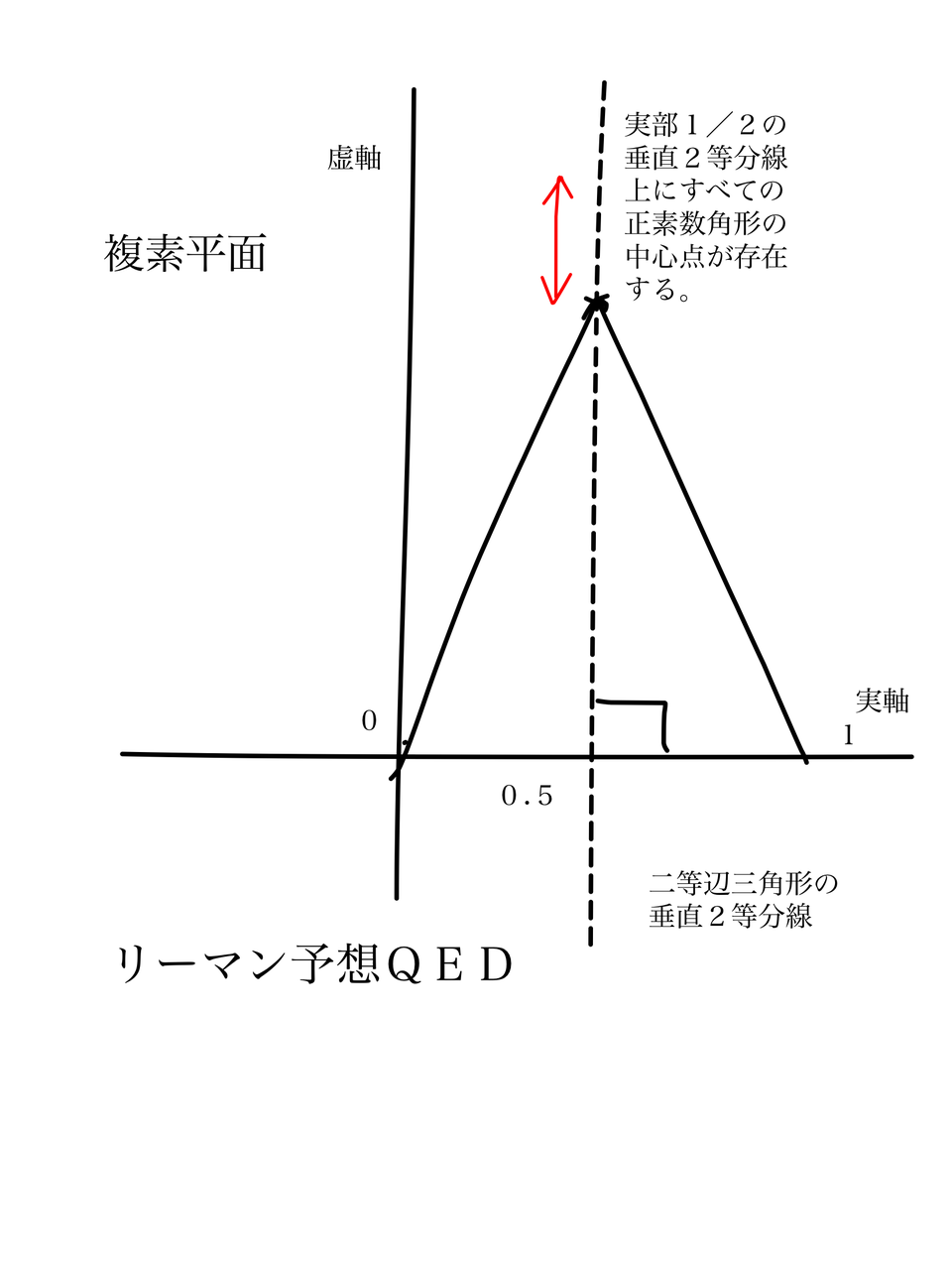



任意の角のn等分と正n角形の作図方の先にあるリーマン予想qed 発想力教育研究所 素数誕生のメカニズム
計算すると、 4 9 = c × c 13 = c × c よって、長い辺の長さは c = 13 (二乗して 13 になる正の数)となります。 では、 13 はどれくらいの長さでしょうか? 3 × 3 = 9 c × c = 13 4 × 4 = 16 なので、 13 は 3 より大きくて 4 より小さい数だと分かります。このように,相似な三角形は対応する辺の比が等しいので,辺の比さえ分かってしまえば, どのように大きな三角形の辺の長さも,すぐに求めることができる。 直角三角形の場合,直角以外の1 つの角が決まると相似となるので, 直角三角形abcにおいては、 bd:dc=ab²:ac² でした。 したがって、 bd:dc=169:81 です。 2乗すればいいだけですね。簡単です。 三平方の定理など他にもいくつかの方法で解くことができますが、これを知っていれば数秒で終わります。




授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf
というわけで 鋭角、直角、鈍角 それぞれのときに辺の長さにはどのような特徴があるかをまとめておきます。 直角三角形の場合 斜辺の長さの二乗が他の辺の二乗の和に 等しい でしたが 鋭角三角形の場合 一番大きい辺の長さの二乗は他の辺の二乗の和より 小さい 鈍角三角形の場合 一番大きい辺の長さの二乗は他の辺の上の和より 大きい大半の書物や 三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a,b,c とするとき、次の三つの不等式が成り立つ。 a bc b ac c ab この関係は三角不等式として一般化される。 三角形の2辺の和と差 三角形の3辺の長さについて以下の定理が成り立




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学




黄金三角形による18 シリーズの三角比 おいしい数学



Agriknowledge Affrc Go Jp Rn Pdf




三角定規 Wikipedia




世界でたった一組の三角形 慶大院生が発見 Sputnik 日本




黄金三角形による18 シリーズの三角比 おいしい数学



Http Www Hxwmzx Com Files Pdf




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



誤答から学ぼうシリーズ 余弦定理を用いて三角形を解く ほのぼの数学頑張ろう




正三角形面積計算機 正三角形面積の計算機 Prxbri



Http Eio Shimane Jp Files Original c46aa Pdf




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




14 号 図形板セット Astamuse
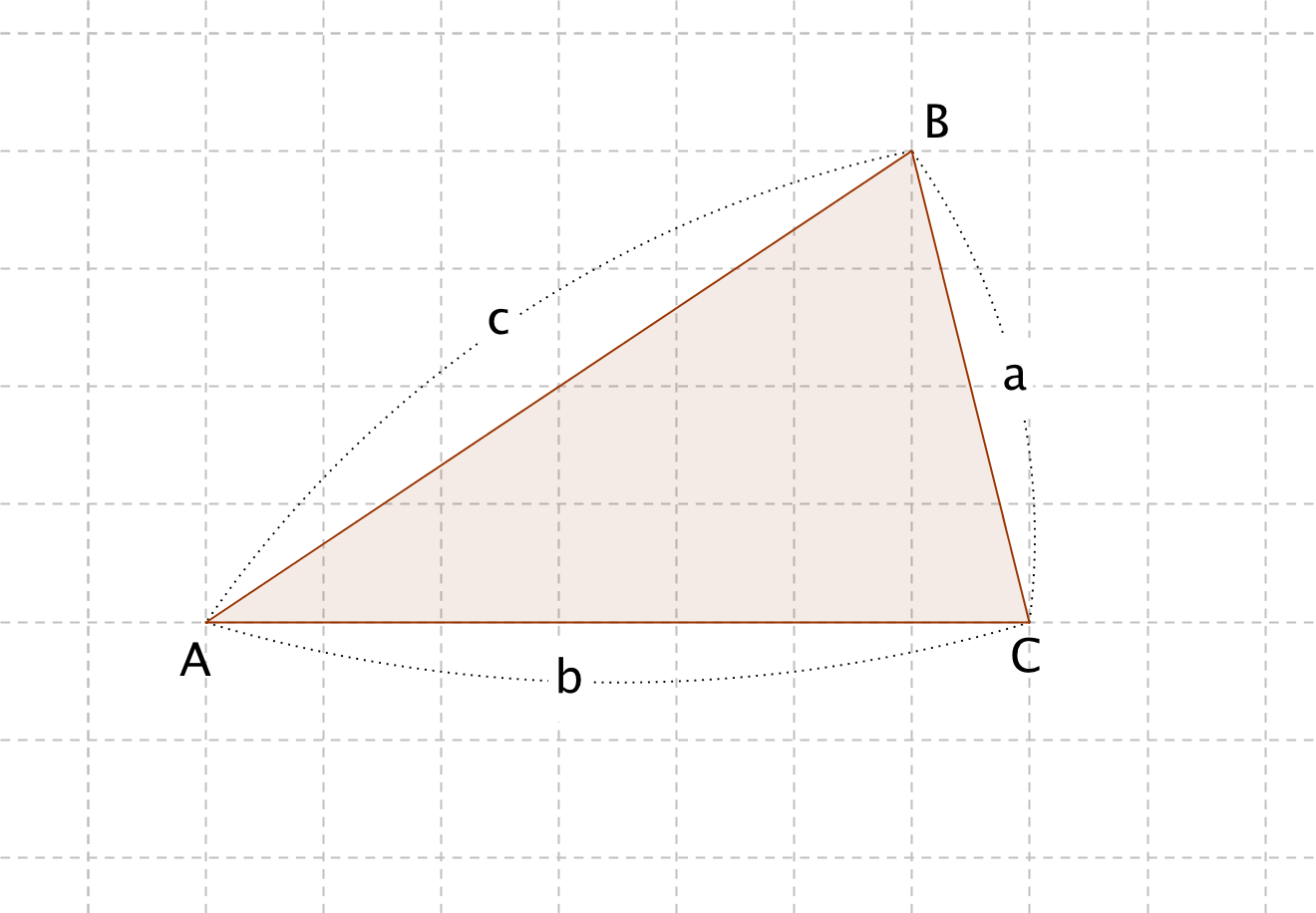



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学



図形クイズ解答用掲示板




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学



2




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




18 絡みの三角比 第1講 黄金三角形の黄金分割 09年度 大阪教育大学




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
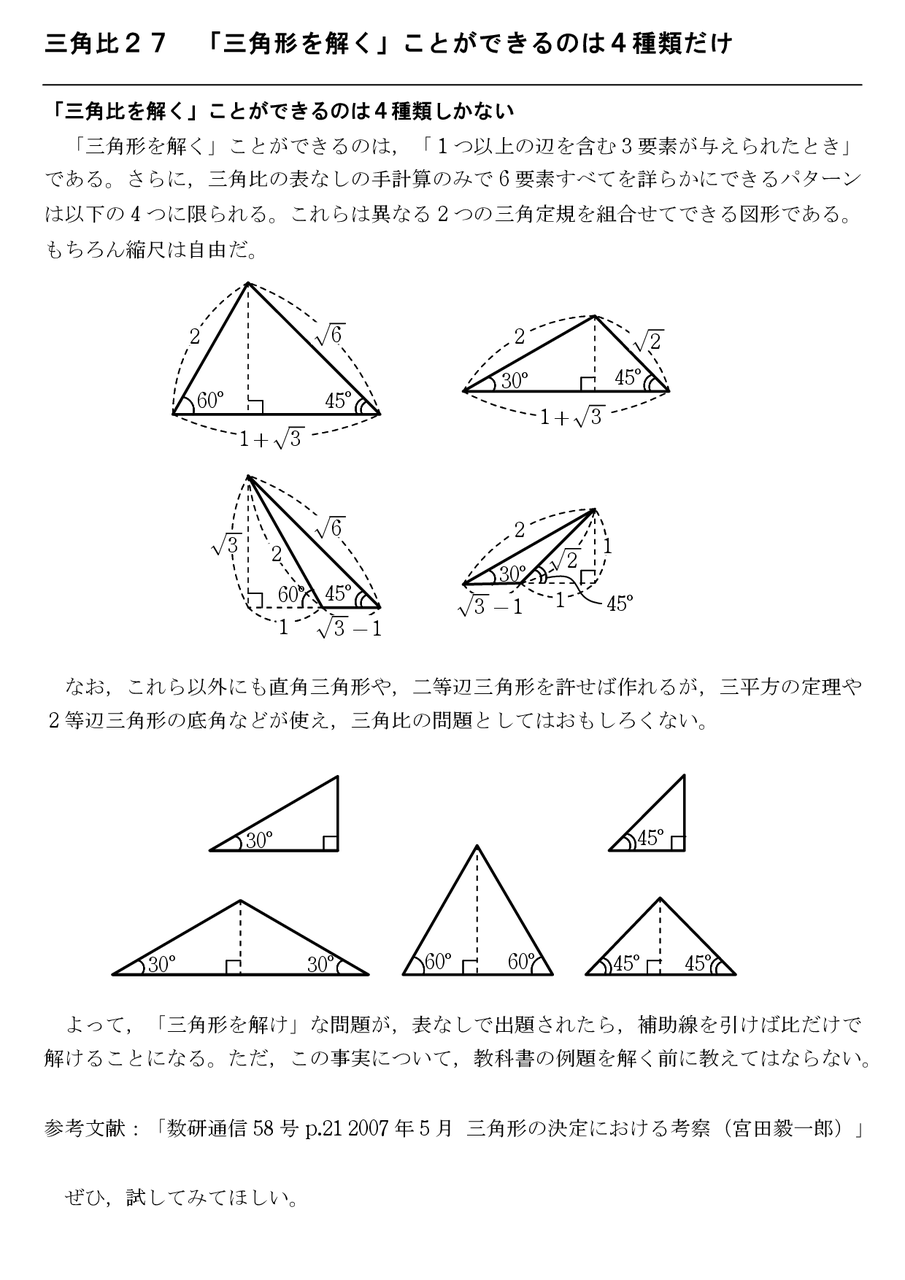



三角比27 三角比を解く ことができるのは4種類だけ 怜悧玲瓏 高校数学を天空から俯瞰する
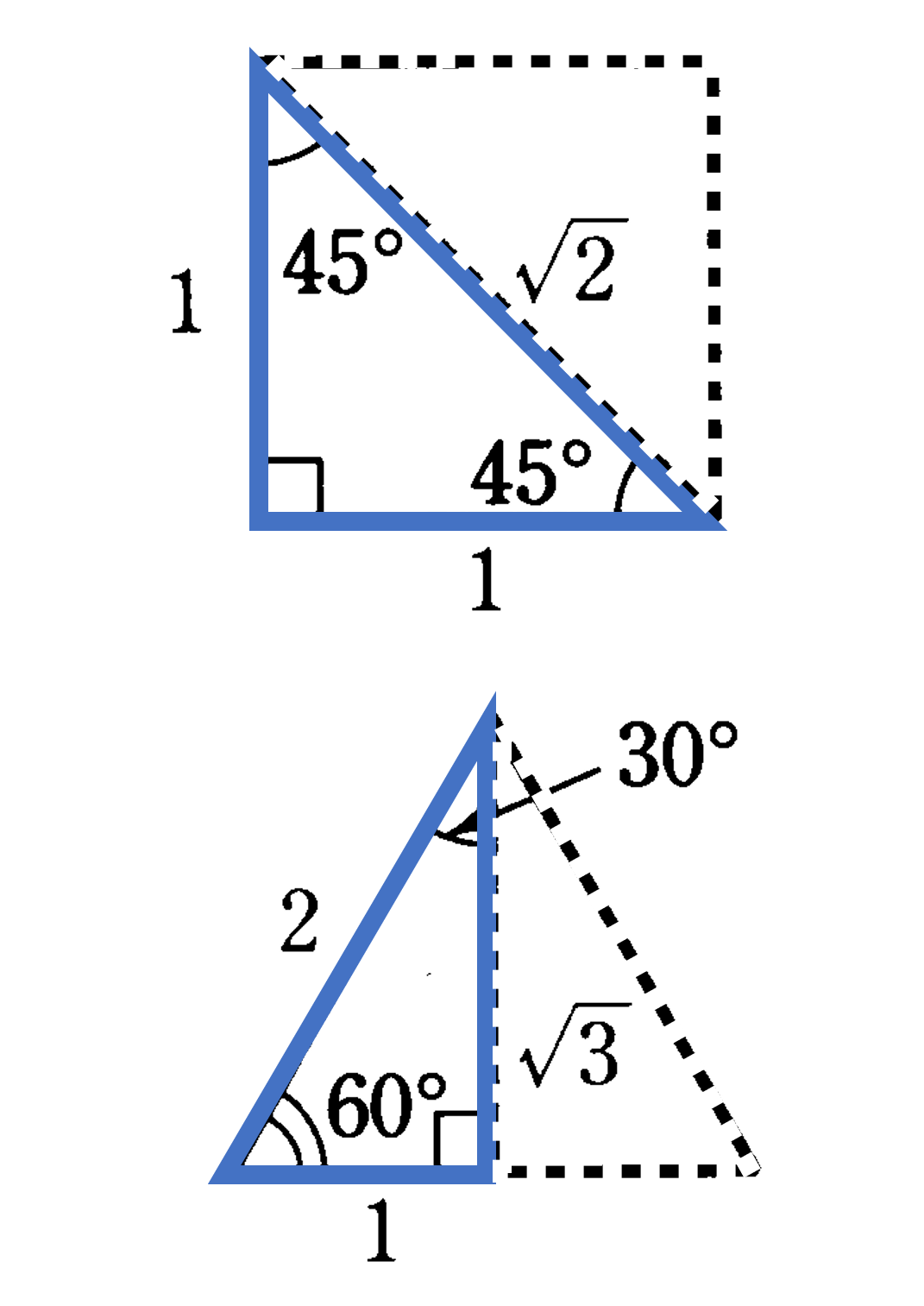



60分で読める中3数学 年版 タカラゼミ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




正三角形面積計算機 正三角形面積の計算機 Prxbri




小5 算数 小5 42 三角形の面積 Youtube




黄金三角形による18 シリーズの三角比 おいしい数学




中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




黄金三角形による18 シリーズの三角比 おいしい数学



2




直角三角形の斜辺の長さを求める 3つの方法 Wikihow




10 号 モデルデータ作成装置 モデルデータ作成方法 物体認識装置 及び物体認識方法 Astamuse
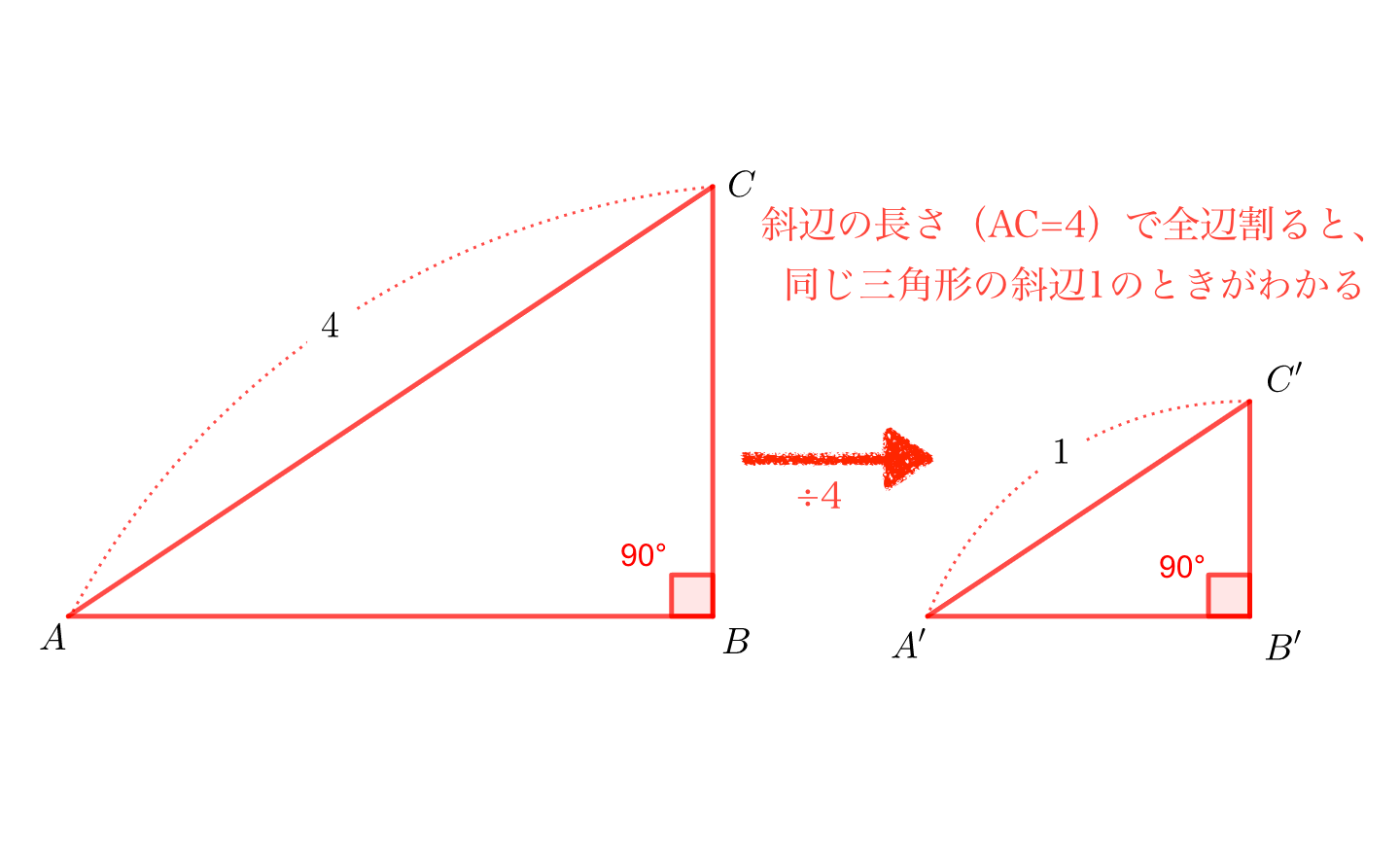



中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック



Agriknowledge Affrc Go Jp Rn Pdf
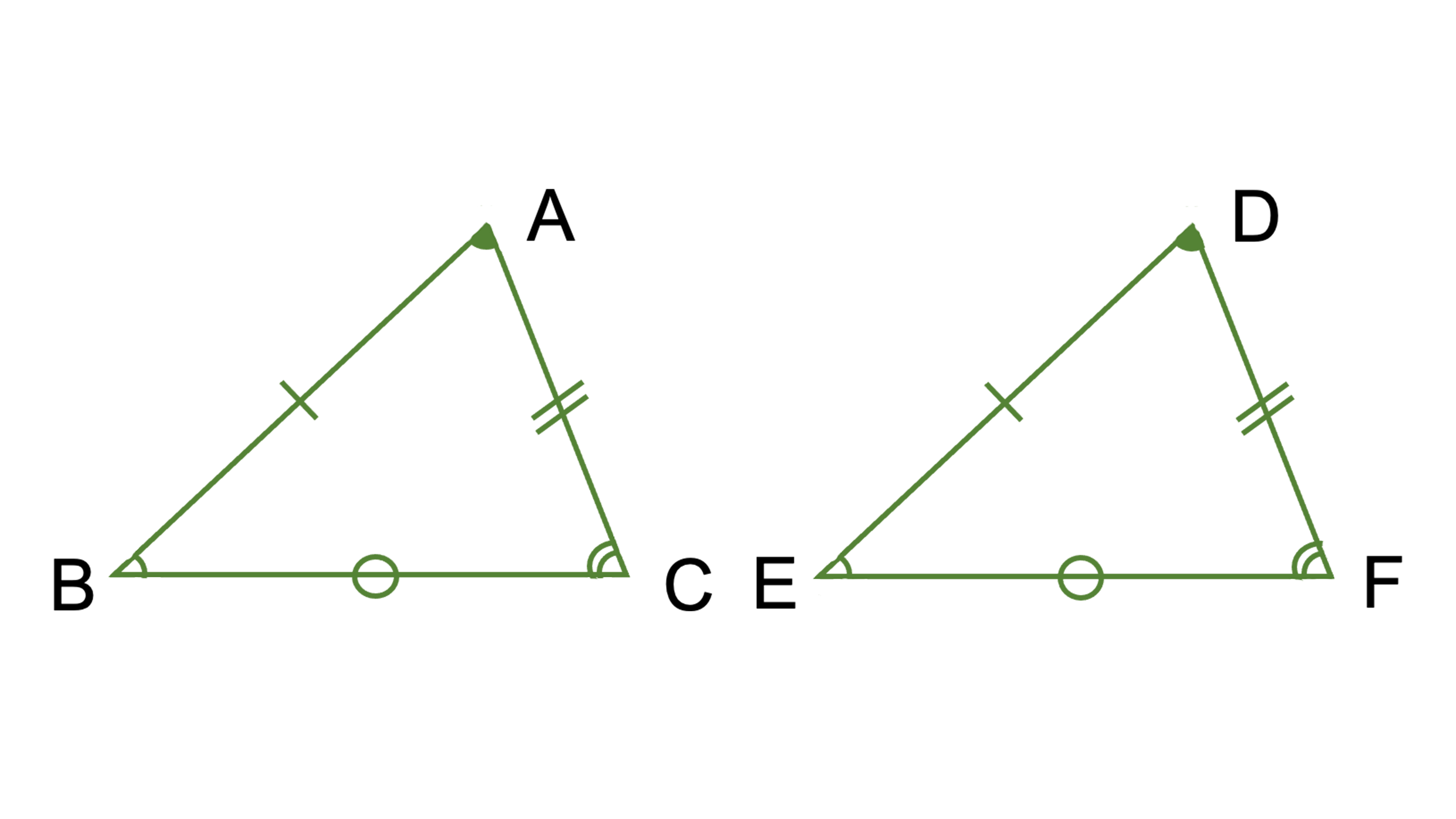



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Tabunka Or Jp Smd Process Download 1 Download Id 4964




収蔵品no 013 任意の角の3等分定規 3連リーマン定規 算数 数学面白グッズ博物館 2117 Since 17 11



Http Web Edu City Yokohama Jp Sch Kenkyu Es Sansu Pdf Jugyouken H30 Simosueyosi30 Pdf




小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ




高校 数学 三角比29 三角形の面積公式 8分 Youtube



Http Www Edu C Pref Miyagi Jp Midori Gakuryoku Plan Pdf A Pdf 9nen A 9 All Pdf




直角三角形面積 直角二等辺三角形の面積を求める公式は Xhymp
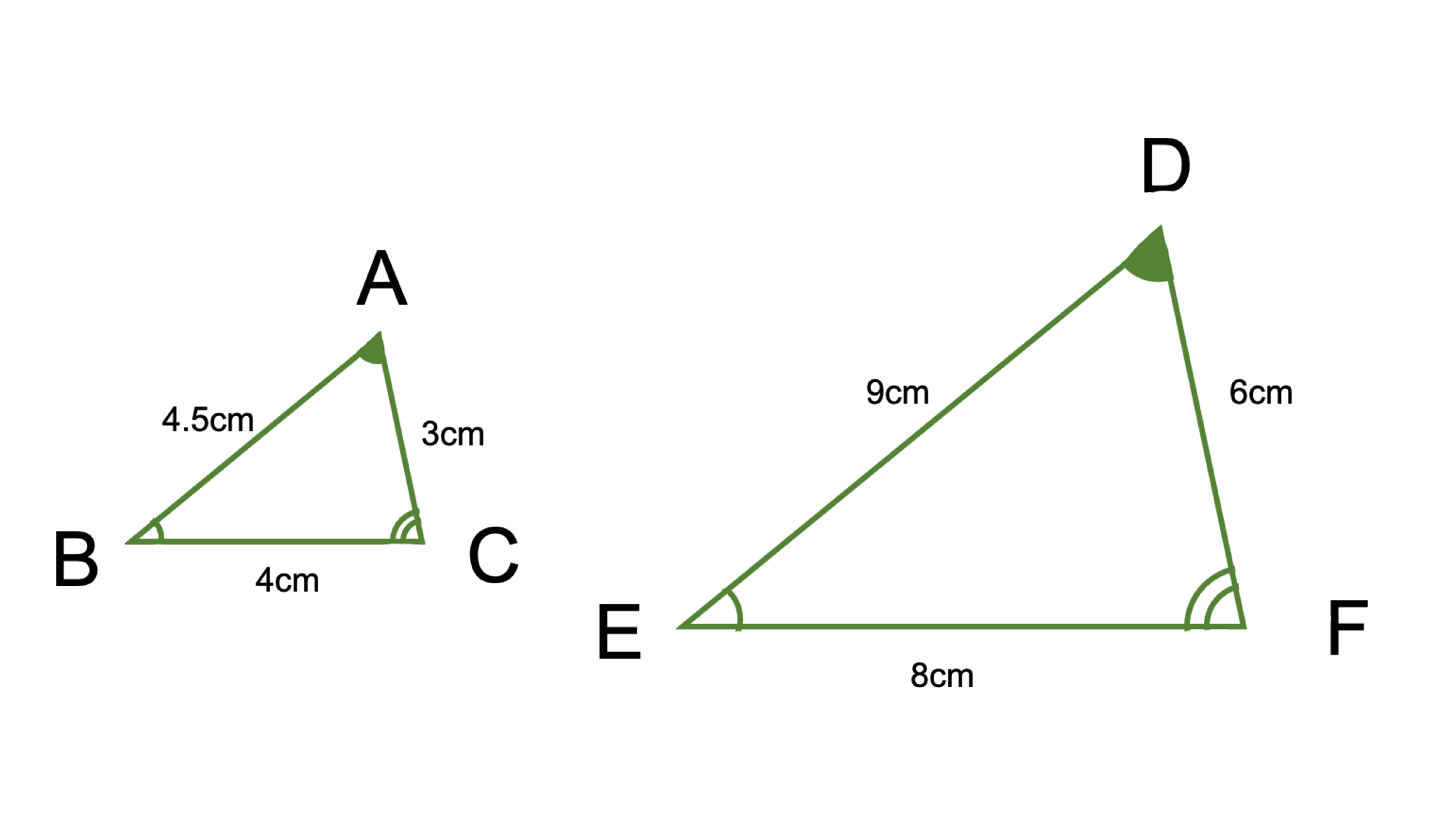



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




図の問題 二等辺三角形 がわかりません この図の回答を 解説付きでお願 Okwave




収蔵品no 013 任意の角の3等分定規 3連リーマン定規 算数 数学面白グッズ博物館 2117 Since 17 11




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
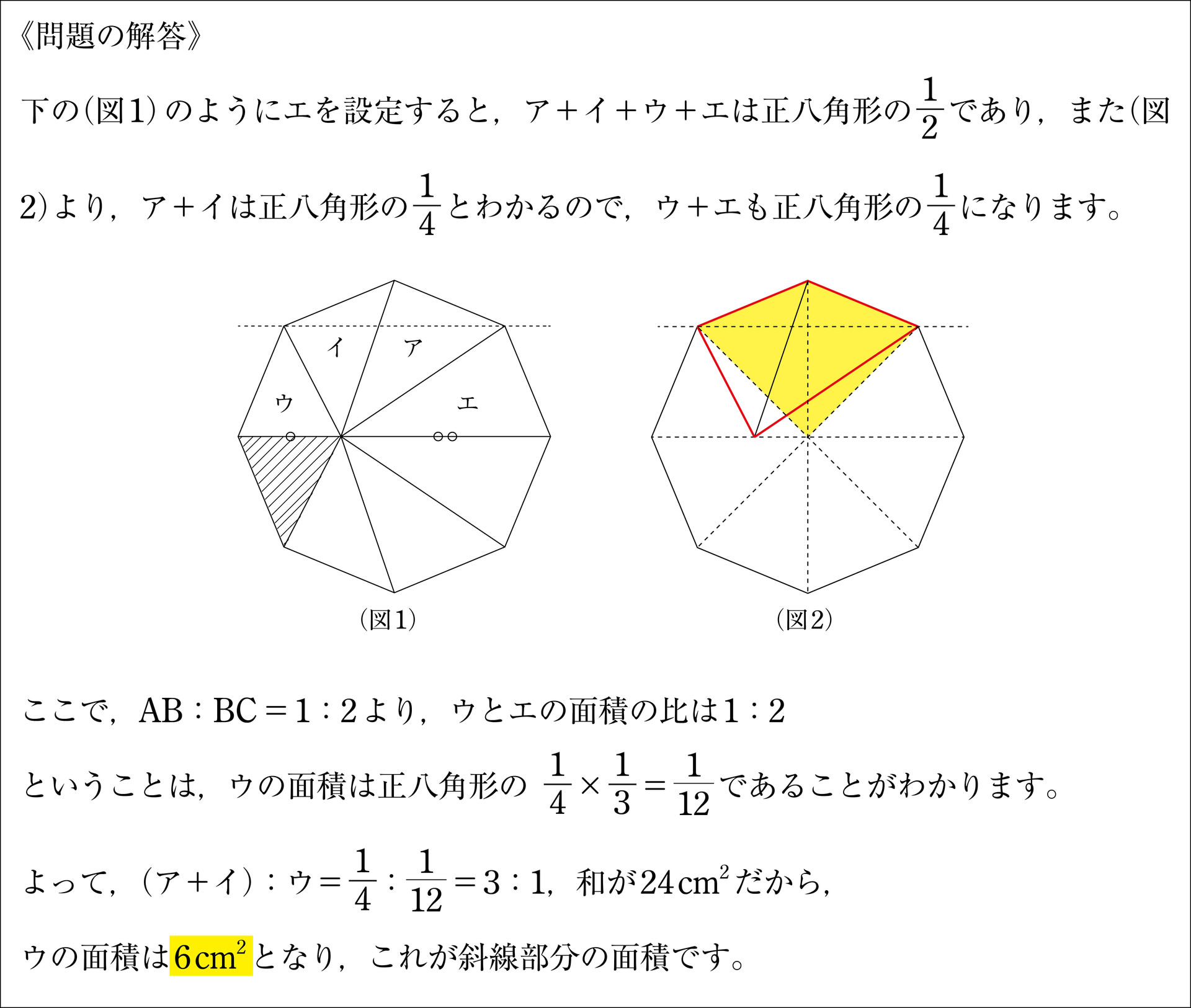



算数ときどき数学 4ページ目



3



Http Web Edu City Yokohama Jp Sch Kenkyu Es Sansu Pdf Jugyouken H30 Simosueyosi30 Pdf



Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo27 27 Tanuma Pdf




黄金三角形による18 シリーズの三角比 おいしい数学




鋭角三角形 Wikipedia




三角形 Wikipedia




黄金三角形による18 シリーズの三角比 おいしい数学



Q Tbn And9gcszi6hqnyyprzvdorpobx8pkyyrcvsogy09fefhpat Py63yhd6 Usqp Cau




積分定数 超算数 陰山氏は 正方形は長方形ではない 正三角形は二等辺三角形ではない という誤った認識を持っている




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
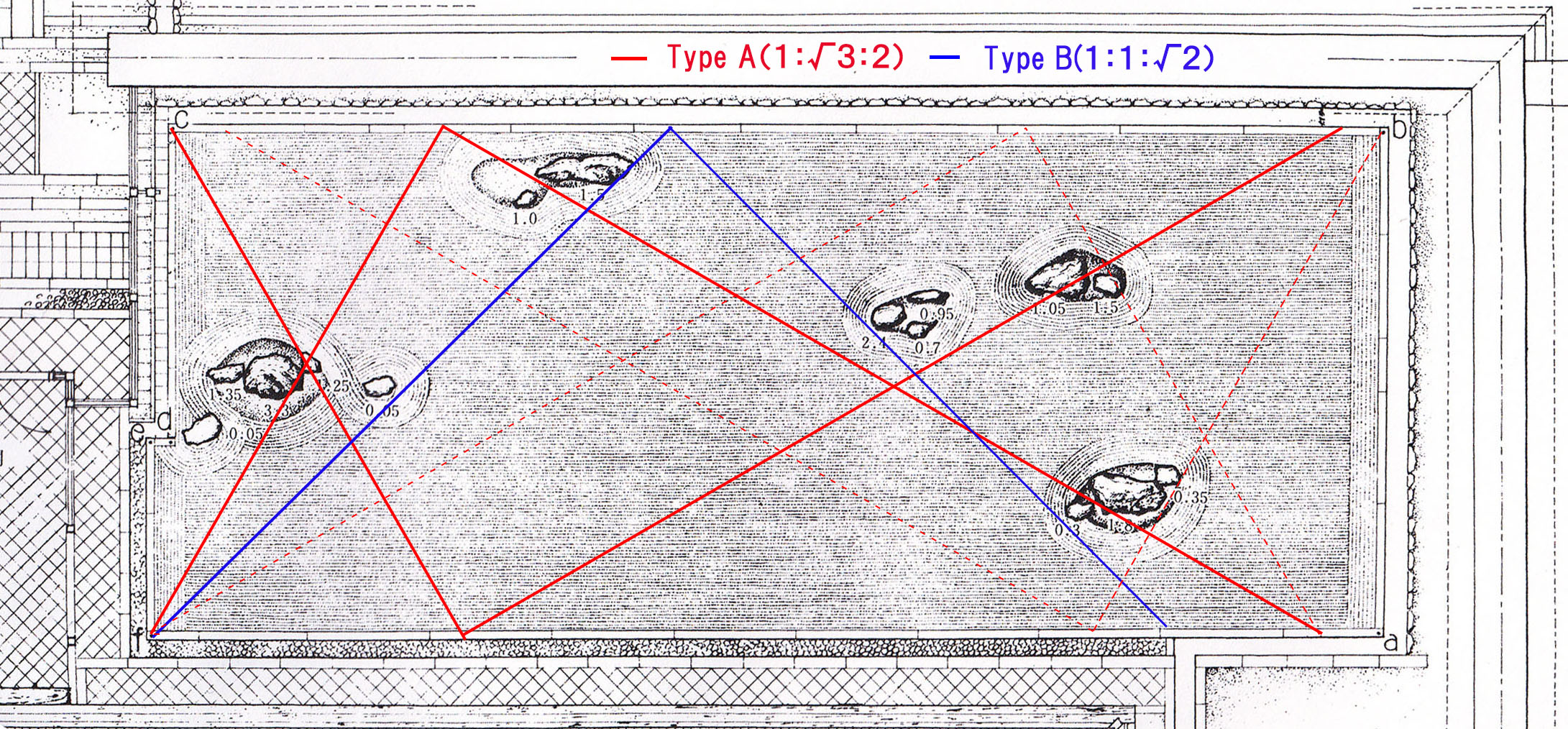



連載 芸術とスタンダール症候群 2 龍安寺の石庭を解明する 2 En Soph



Http Www Orion Metaphysics Com Wp Content Uploads 12 04 Ec7ce114ff99a97c18a11aab03fd7316 Pdf




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




Cometのサボテン栽培日記 頭の体操




直角三角形の辺を求める Youtube




14 号 図形板セット Astamuse




黄金三角形 Wikipedia
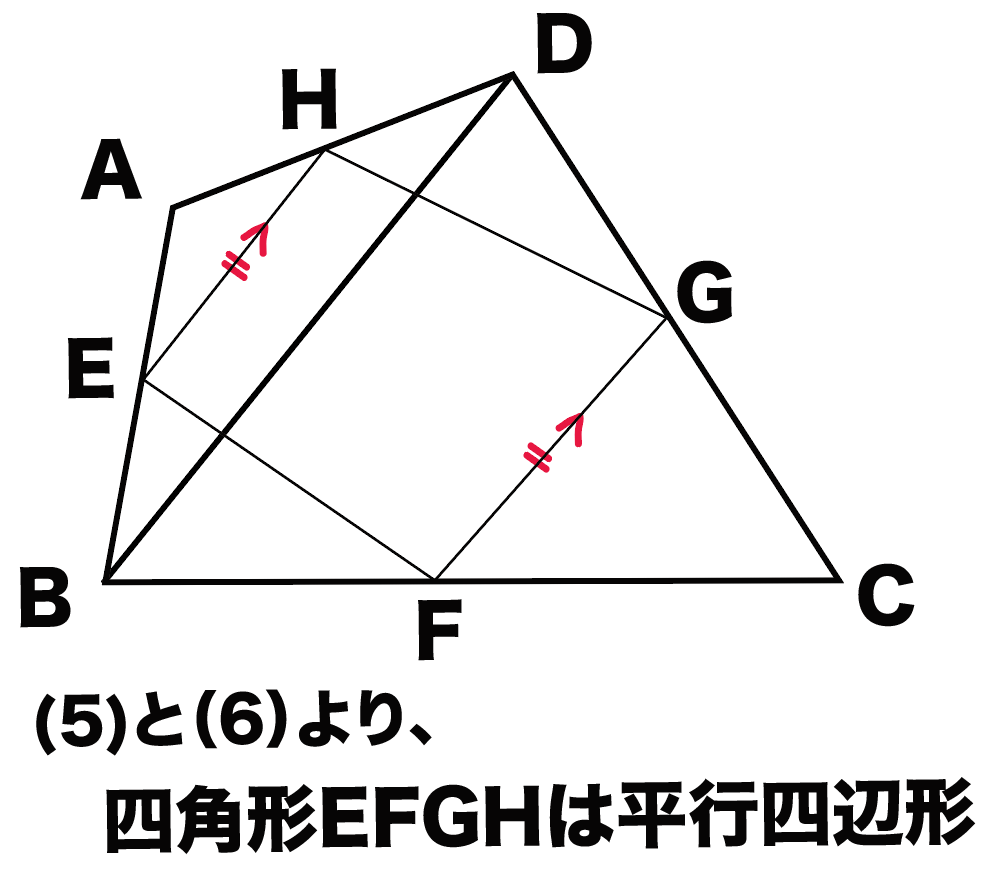



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




図の問題 二等辺三角形 がわかりません この図の回答を 解説付きでお願 Okwave



1



図形クイズ解答用掲示板




14 号 図形板セット Astamuse




1 の問題で 自分の証明でも合ってますか 字が汚くてすいません Clear




三平方の定理 覚えておきたい基本公式を解説 数スタ



2
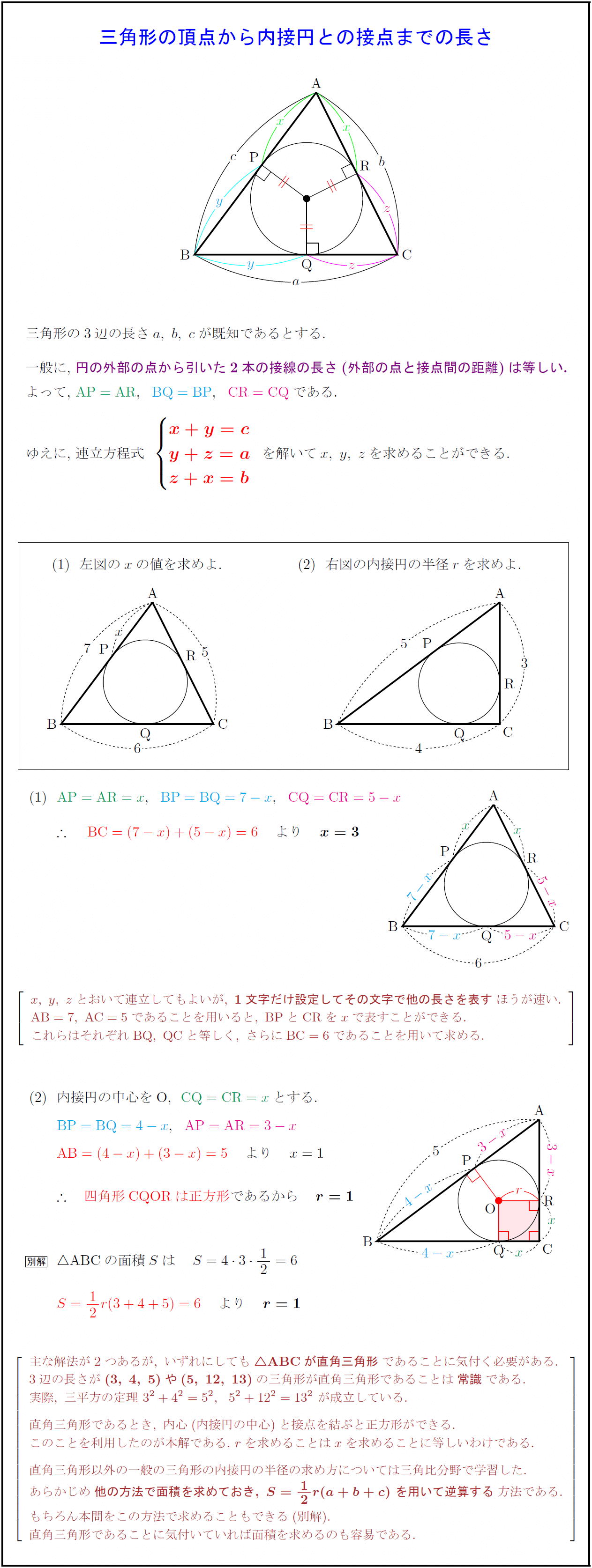



コレクション 三角形 辺の長さ 求め方 小学生 シモネタ



1



三角定規




14 号 図形板セット Astamuse



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf




図形の相似 Wikipedia



2



Tabunka Or Jp Smd Process Download 1 Download Id 4964




数学 中3 61 三平方の定理 基本編 Youtube



Http Www Ikushin Co Jp Shuppan Textimg 17matokan Chuhyo Sugaku Hon Pdf




中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック



三角形の2辺の和と差
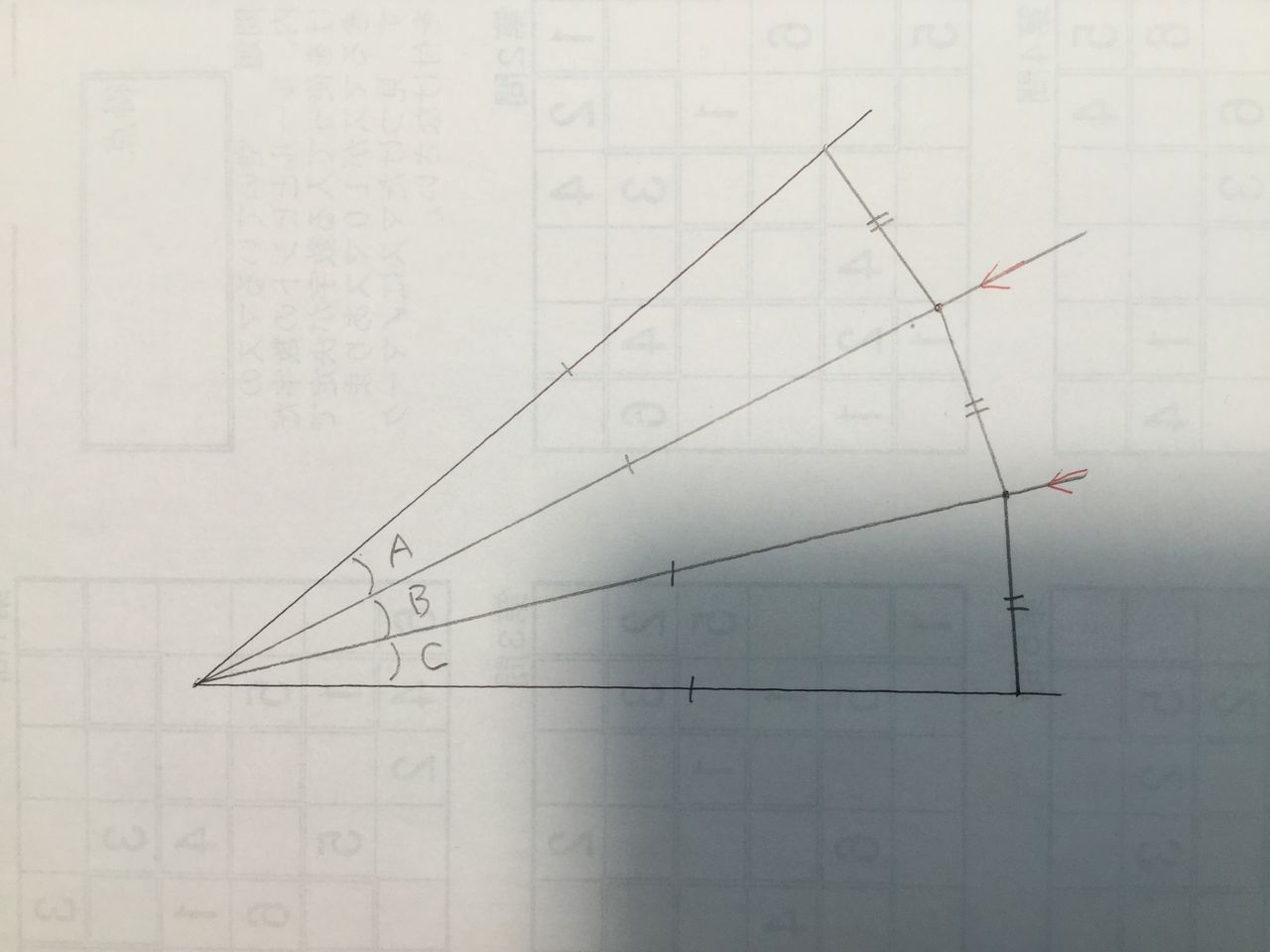



収蔵品no 013 任意の角の3等分定規 3連リーマン定規 算数 数学面白グッズ博物館 2117 Since 17 11
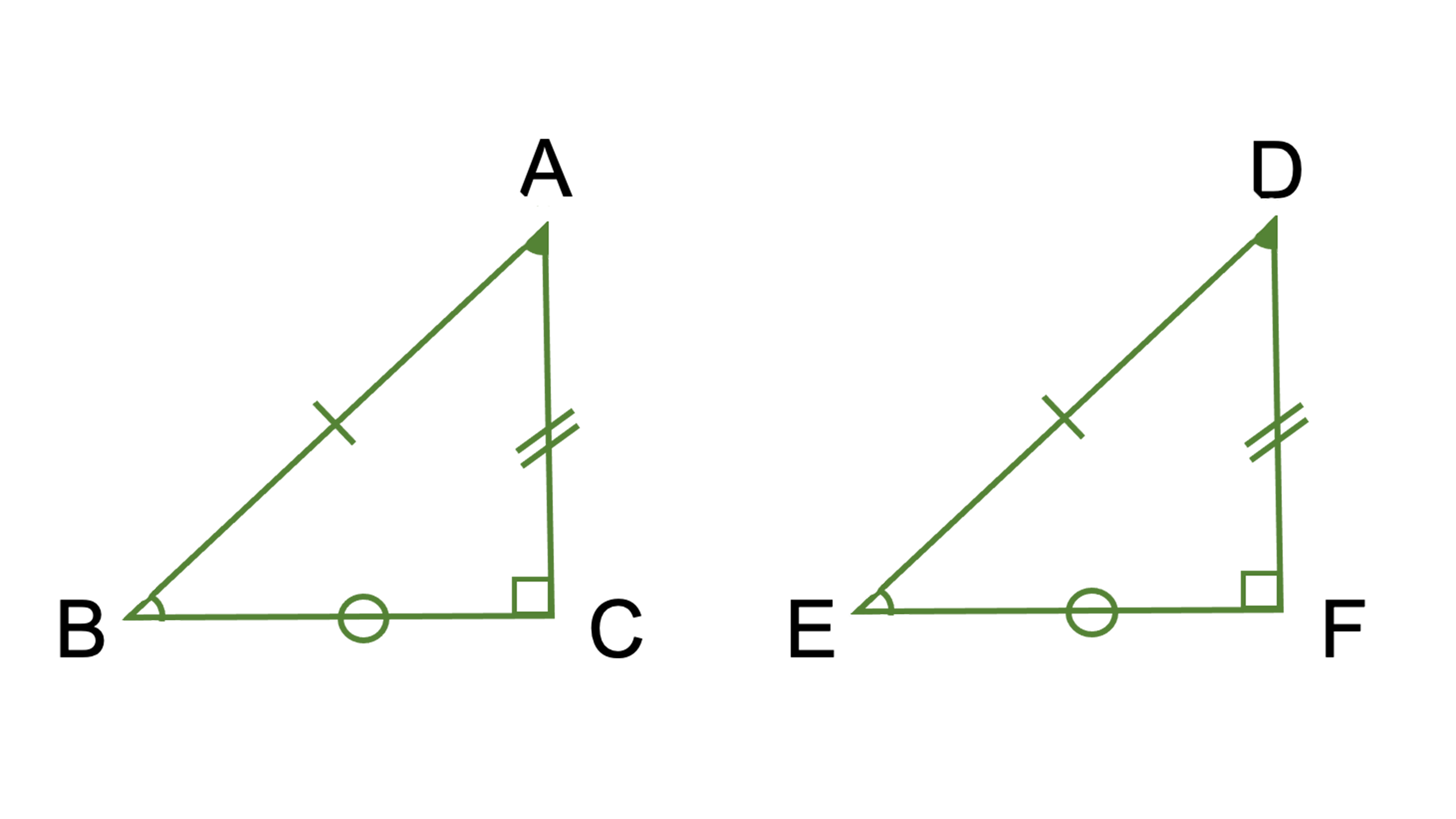



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
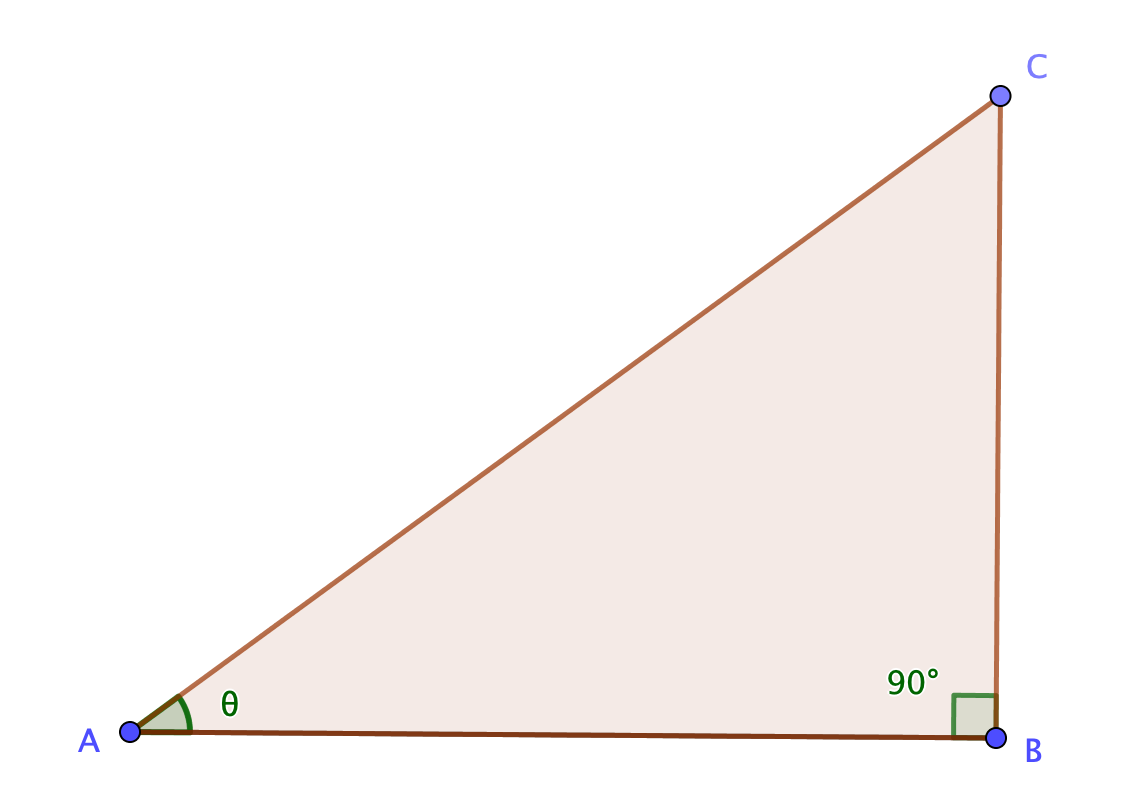



中学生でもわかった サインコサインとは 公式を暗記しなくても 感覚でわかる 青春マスマティック




慶應義塾大学の大学院生が発見 世界でたった一組の三角形 大学ジャーナルオンライン



Http Www Nikkei Com Edit News Special Gakute Chugaku Kaisetsu Suugaku3 Pdf
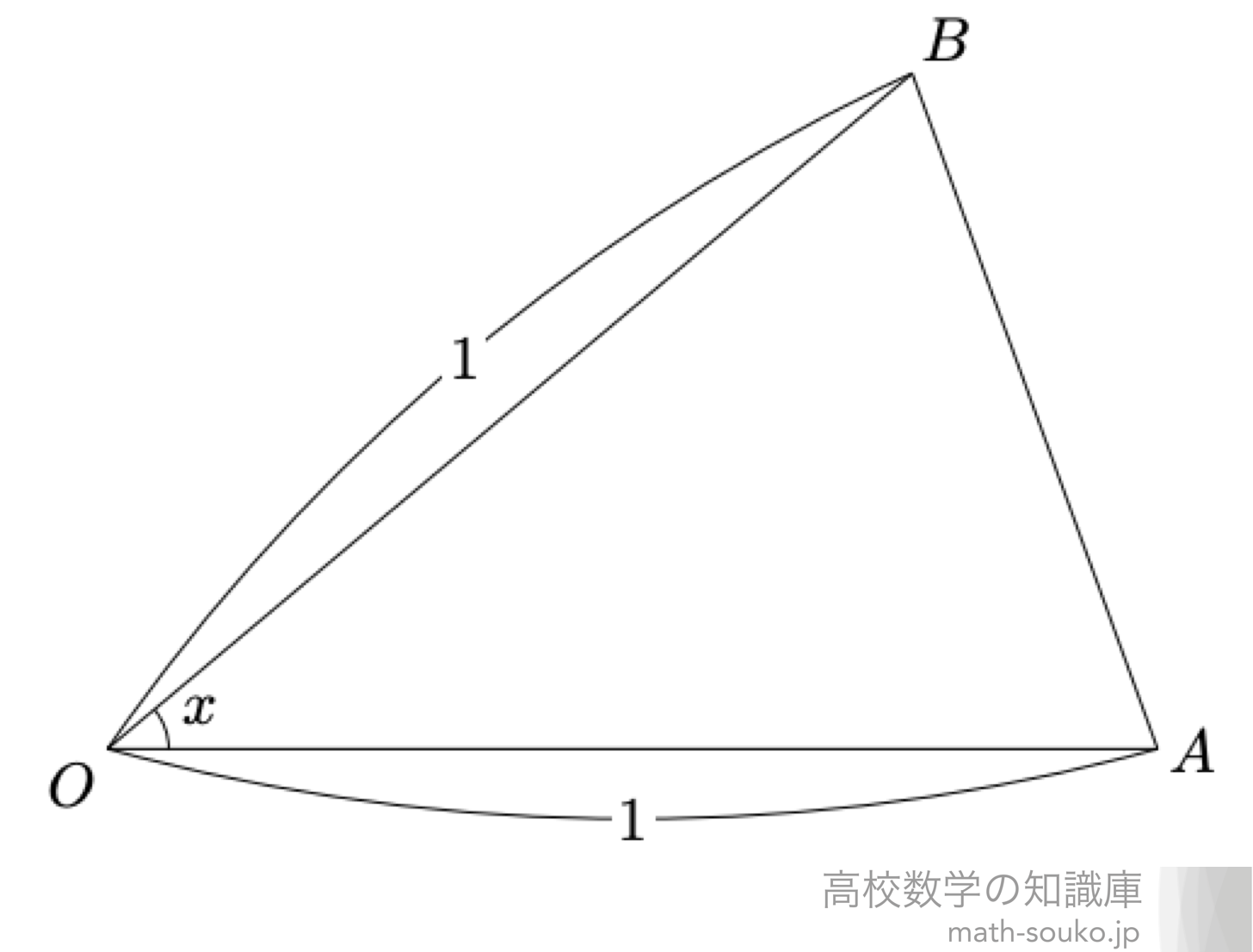



三角関数の極限公式の証明とその使い方 高校数学の知識庫




チャート数1 Clear




六角形の面積を求める 4つの方法 Wikihow



0 件のコメント:
コメントを投稿